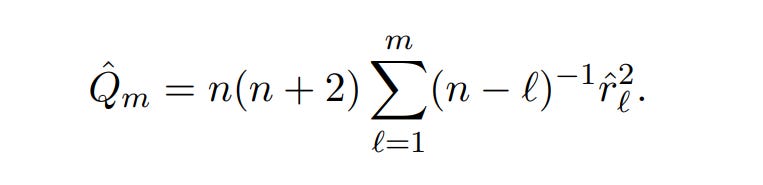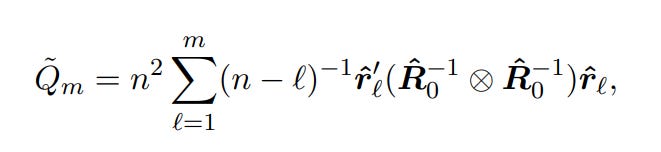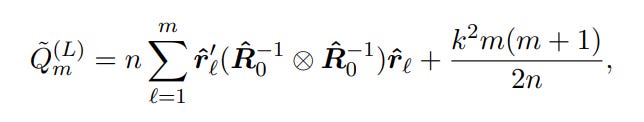Monte-Carlo Minimization for Synthetic Portfolios

Forming synthetic mean-reverting portfolios (MRPs) using Monte-Carlo Minimization (MCM)

Feb 10, 2023

Introduction

Monte-Carlo Minimization (MCM), also known as Basinhopping is a popular non-convex optimization algorithm for global optimization. It is derived from the chemical physics literature and is accompanied by Dual-Annealing as its primary alternative.

Today we will apply it to digital asset markets to form synthetic mean-reverting portfolios by optimizing for multiple different mean-reversion tests. This article merely is meant to provide a methodology for generating these portfolios and we will not explore the optimal trading problem needed to form a full strategy. There are also many backtesting caveats that are beyond the scope of this article that would need to be explored separately first.

Data

We use these below assets in our analysis, but this is entirely an arbitrary selection. This research blog will likely explore universe selection methods in future articles. Research relating to optimization and mean-reverting portfolios will be explored in a mix of both free and paid articles, alternating each time.

The table below gives an overview of the dates used. There hasn’t been much of a significant change in the effectiveness of this technique, so we can use older data. This was also influenced by this dataset being the first one I found on my computer.

These are close prices arranged as a matrix which is usually required for such optimization problems, especially the more complicated convex methods we will explore in later articles.

Normalization

In the interest of avoiding as much look-ahead bias as possible, we standardize our training and test sets individually.

This is the below-standardized training set:

For clarity, we are using the below formula where x is our asset close prices, mu is the mean of our prices, and sigma is the standard deviation of our prices. For shorter-term synthetic portfolios standardization is ideal, but for longer-term portfolios, it can make our portfolios less robust as volatility changes over time.

We also show our testing dataset that has been standardized here.

Objective Function

We will be optimizing for mean-reversion using the portmanteau statistic which is used to test for the presence of white noise in time series.

It is formulated below:

As some readers may notice, we are using the 1978 Box-Leung formulation of the statistic and not the original 1970 Box-Pierce formulation shown below:

For further improvements, the additional options of the Hosking portmanteau test formulation (1980) or the Li and Mcleod formulation (1981) could be used.

Hosking:

Li and Mcleod:

The final two I suggested are not appropriate for this use case because of their increased complexity. One of the primary reasons that the Portmanteau statistic was chosen was because it is efficient to compute when compared to statistics like Augmented Dickey-Fuller. Despite its computational efficiency, it is still vastly superior to ADF when used for lower timeframes.

Portfolio Optimization

We use the SciPy Optimize library which includes both Monte-Carlo Minimization (named as Basinhopping in the library) and Dual-Annealing. There is already some literature on the use of Simulated Annealing for the formation of mean-reverting portfolios, but since its release, Dual-Annealing has proven a much more effective and popular solution. Overall, it is regarded that Monte-Carlo Minimization is more effective than Dual-Annealing in chemical physics, but it is yet to be determined whether this is the case for financial markets.

Using the library with custom-defined optimization metrics we get the following results:

We then generate this mean-reverting portfolio. The training set is shown in blue with the out-of-sample data shown in red.

Taking another arbitrary data window, but here halving the size of the train and test sets respectively we were able to achieve similar mean-reversion.

Final Remarks

We find in our analysis that whilst our portfolios do tend to decay out of sample they remain highly mean-reverting. This is a trend that was found consistently with other non-convex optimization approaches I have used before to do this. This effect typically only occurs for shorter timeframes. Usually, you get a total decay when you do not use ultra-robust methods for creating mean-reverting portfolios over longer timeframes. This method is likely one of if not the least robust of them all.

It is however a novel application of a very underrated algorithm to financial markets and we were able to generate highly mean-reverting portfolios both in and out of sample despite seeing some decay. The dynamics of short-term pairs trading are very different from longer-term pairs trading portfolios that the literature focuses on, and for shorter-term pairs trading portfolios stationarity / robustness is less of a concern as we quickly generate new portfolios, capturing temporally local effects.

It is important to note that as a result of using assets that are not top 15 liquid coins, there will be lower capacity in this strategy. We also have to trade many assets which further increases the costs of trading large sizes. This is likely only appropriate for smaller capital bases. The volatility and increased mean-reversion exhibited by medium-sized coins are ideal for our research. You may also maximize the objective to try and form index portfolios for different areas such as DeFi tokens etc, this is best done with PCA-based methods which we will explore in one of the next articles!

Eager readers may want to continue experimenting with this research topic and finding ways to trade these mean-reverting portfolios optimally and cost-effectively.

If you enjoyed reading this, then feel free to subscribe. The next article will be paid as I alternate between a paid and unpaid article each time.

The Quant Stack