Truncation Method for SMRPs
Sparse Mean-Reverting Portfolios generated with the truncation method.
Introduction
We will be building off the previous article on non-sparse synthetic portfolios and look at the truncation method for generating sparse mean reverting portfolios. This is part of a 3 article series where we start with a non-sparse method and then climb into some heuristic approaches to sparsity. Our first heuristic approach is the truncation method. This is quite an easy method to understand so this should be a comfortable introduction; I’ll also be including code so that readers can follow along themselves.
As with before, we will be using a pre-defined set of stocks in the S&P500 that are all in the same industry. Keeping the data the same should help for easier comparison.
Data
Since the data is the exact same data as the previous article, with the exact same train and test periods, there is no need to explain it again. Readers are free to reference back to that for more information on how the data is organised.
Methodology
The Truncation method is probably the simplest of all. To start, we calculate the non-sparse solution with all the tickers as we did in the previous article. Then we normalise our weights (for the minimum eigenvalue weights) by the price of each asset. Take the absolute value, rank them largest to smallest, adjust them so that they total to 1 (thus, our weights are the % contribution to the notional volume needed to trade this portfolio), then select our top x tickers by contribution.
We can then retrain on this new, truncated, set of assets or we can skip this step and leave the weights unchanged (using the real weights of course, not the adjusted & absoluted wieghts as those only represent each asset’s contribution).
For our example, we will take the top 5 assets by contribution. We end up only discarding about 5-10% of the notional volume, but remove more than half the assets. This lets us achieve a relatively sparse portfolio, and we will see that the portfolio that wasn’t retrained is stronger OOS. Less is more in many cases, and reducing the amount of fitting we perform is a great way to ensure robust portfolios. When the discarded % is this low we are able to do this, but only because these components are noise that have no effect on our OOS portfolio.
The simplicity of this method makes it easy to understand / implement. Our next article will cover the greedy method which is a little bit more work, but is a far better method.
Truncation is super fast to compute, making it the fastest way to build sparse mean-reverting portfolios. This is ideal for working with large datasets, but otherwise greedy is superior, something we will show in the next article for this series.
Implementation (CODE)
I am starting off from the same place as before (reference previous article) with the exact same data, exact same weights, and exact same non-sparse portfolio.
eigvals, wgts = portmanteau_gep(df_train, 10)This is the same method we coded up last article, and when we plotted our minimum eigenvalue portfolio we returned this:
We start by creating our adjustment factor, we then use this to form our contribution list as explained in the methodology.
The reason we multiply by adjustment factor divided by itself (basically all ones) is to take our weights from a numpy array with no tickers attached to a pandas array where the index is our ticker names. They are aligned in the same order so this is fine. Doing this lets us select the unadjusted weights by ticker which is easier. My approach is a very dirty way to do it, but hey it works. I also have infrequently used this model in my research due to the superiority of the greedy method (hence the dirty code), but insights about how non-sparse methods can overfit weights are revealed a lot more intuitively in our results so well worth learning.
Finally, normalize the contribution list so that all values total 1 (thus representing the % of notional volume each ticker contributes).
# Take mean of each asset, then divide by average price to normalize values.
adjustment_factor = df_train.mean() / df_train.mean().mean()
# Divide our weights by our adjustment factor, absolute them, then sort.
contribution_list = abs(wgts[0] / adjustment_factor)
contribution_list = contribution_list.sort_values(ascending=False);
# putting our weights into pandas with tickers attached (dirty af)
ticker_weights = wgts[0] * (adjustment_factor / adjustment_factor)
# Normalizing so all total to 1
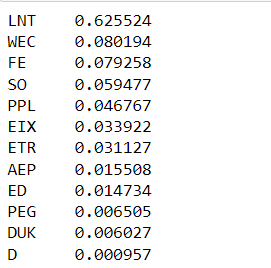
contribution_list /= contribution_list.sum()Below is our contribution list, we take the top 5, which means we are only losing about 10% of the notional volume, contributions which are effectively noise.
sparse_tickers = contribution_list[:5].index.tolist()
sparse_weights = ticker_weights.loc[sparse_tickers].values.tolist()We take the top 5 tickers to get our sparse tickers, then we use the ticker weights (our actual weights which haven’t been changed short of the redundant transform - multiplying by 1 - we did to add tickers as the index).
The above list is our final set of tickers, our sparse tickers. Plotting the portfolio (using the original wieghts) we get the below results out of sample (we have been using df_train so far, this chart is df_test).
Our above porfolio is actually more robust than the prior portfolio because we have removed the useless assets. As shown below when we take the remaining assets and use them instead, they create a drift term which actually hurts our results:
Some mean reversion, but mostly drift. This is likely why our sparse portfolio appears much more stationary out of sample than our non-sparse portfolio.
Looking at our retrained portfolio we quickly re-run the code, as shown below:
eigvals, wgts = portmanteau_gep(df_train[sparse_tickers], 10)and then we plot our new portfolio and achieve this porfolio out of sample:
The portfolio in-sample:
We only have one example here, and the jury is out on whether retraining is a good idea, it probably is in my view, but we ran into the same issue that we previously were trying to avoid where a large majority of the weights are basically noise because the non-sparse method finds a weight for every asset in the portfolio, overfitting some when they should just be 0. This results in a few being very small weights which barely contribute to the portfolio, but help overfit towards our objective of minimising portmanteau (only in-sample, out of sample this overfitting comes to life and they actually hurt more than they help as we saw).
Conclusion
We looked at a very simple method for making portfolios more robust and reducing turnover. We also showed the ugly side of non-sparse portfolios where the majority of the weights are overfit noise which do not contribute significantly to the final portfolio. This is a fantastic example of how quick and dirty methods can vastly improve performance by avoiding unneccessary fitting.